Irrazionali

“Ho un problema che mi assilla, posso?” Mi fa gentilmente uno studente di liceo prendendo in mano il gesso, “Vede: se si prende un quadratino qui sulla lavagna, e si disegnano due lati che misurano uno, e poi si traccia la diagonale. Calcolandone la misura viene fuori radice di due. Ed è la misura precisa di un lato, che è finito. E allora perché la radice di due ha un numero infinito di cifre dopo la virgola? Come è possibile che un lato finito sia descritto da un numero che ha infinite cifre?”

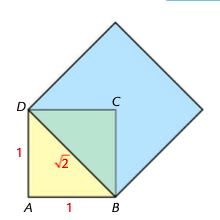
Guardo lo sguardo infervorato e scorgo l’attimo della scintilla, accesa da colui che continuerà a cercare, a togliere veli o strati superficiali di buccia per andare oltre. Come Talete, come Pitagora, come Cantor, come Gauss, come … Non come me certo. Che posso solo testimoniare la bellezza di quell’attimo, in cui nel pensiero in formazione, in evoluzione, negli anni dell’adolescenza, si affaccia l’idea dell’irrazionale. Perché di questo si tratta. Di quando la certezza della misura si scontra con un posto che non c’è. Dove lo mettiamo questo numero che non trova posto, non è due, non è tre, e non ha un punto che gli corrisponde sulla retta, pur se fatta di infiniti punti? Non è un caso che a pormi la domanda sia un ragazzo dallo sguardo intenso e a volte spaurito. Sempre attentissimo, eppure corredato da una di quelle certificazioni che si usano oggi nella scuola, per dire che qualcuno o qualcuna ha difficoltà di apprendimento. Forse non legge alla stessa velocità degli altri? Non ha una calligrafia abbastanza precisa? Forse inverte qualche volta le lettere, i numeri? Forse pensa a una velocità che si impenna troppo rapidamente e stravolge la curva, che giace immobile, sul piano cartesiano dei criteri di valutazione?

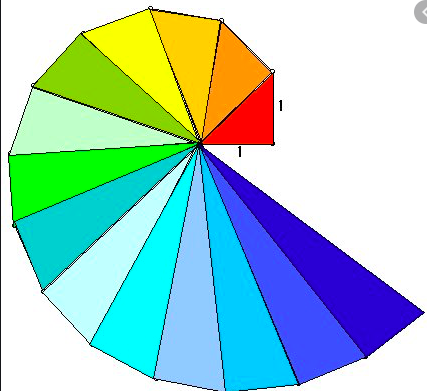
Non lo so, ma lo spunto mi porta in punta di penna. Bentornata a scuola, mi dico. Benvenuta nell’insieme che ci contiene tutti, se abbiamo avuto la fortuna di nascere e crescere in una società dotata della scuola dell’obbligo. Da qualche mese procedo in punta di piedi, sentendomi tutto sommato a casa, in un mondo dove ognuno dovrebbe avere il diritto di essere e provare a esistere, anche le mosche. E mentre lo penso e lo scrivo, un po’ per pizzicarmi le braccia, incerta che non sia tutto un sogno. Mentre mi interrogo sul senso che un’eterna alunna come me si ritrovi dietro una cattedra, nella posizione che non avevo mai avuto il coraggio di occupare, mentre conosco nuovi docenti e nuovi alunni, mi ripasso a mente alcune scene dell’intramontabile film “La Scuola” di Daniele Lucchetti, tratto dai romanzi di vita scolastica di Domenico Starnone. Ripenso a Cardini, alunno protagonista assente a oltranza, ma presente sotto forma di ronzio costante, rumore di fondo, continuo di suono dove collocare ogni nota, anche il fruscio d’ali, anche l’infinita bellezza dello scoprirsi irrazionali, dell’esserlo per definizione, in quell’età di energia potenziale, tutta chiusa in un bozzolo, pronta a liberarsi e trasformarsi nella ricerca che non può finire in nessun punto.

Perché se anche si parte da un’origine certa, come si fa a sapere di aver raggiunto la meta, se il proprio posto potrebbe essere ovunque sulla retta, nel piano o nello spazio di chissà quante dimensioni?

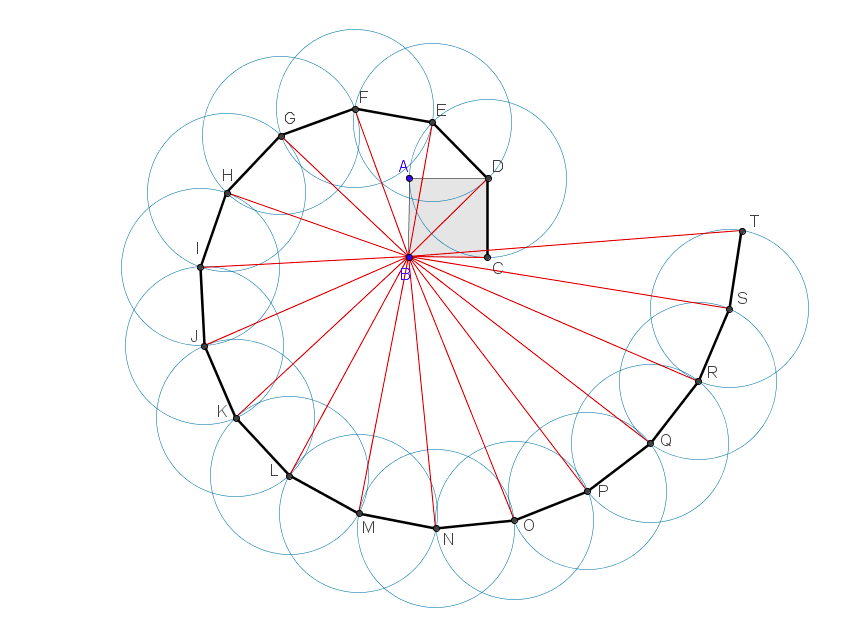
Ma bando alle parole che arrivano facilmente a citare loop o stringhe, senza misurarsi con il quotidiano e con lo studio che ci vuole per sapersi spiegare e provare a spiegare cosa ci sia dietro termini astratti e ingarbugliati. Riflettendo sul rumore di fondo e sulle coincidenze non casuali, ho scavato nelle letture del passato, seguendo un filo di associazioni del tutto casuali. E ho ripensato a un librino che avevo recensito qualche anno fa, molti per la verità, per l’appena nato giornale di scienza online Galileo. Era “Il mago dei numeri” di Hans M. Enzensberger (Einaudi Tascabili). L’autore allora componeva un racconto sulla storia dei numeri, come una serie di sogni di un bambino, che, interagendo con un mago sornione, impara a capire quanto siano ‘irragionevoli’ gli irrazionali, o come ‘saltellino’ i quadrati perfetti, attraverso un castello di metafore inventate dal mago per raccontare la complessità della matematica degli infiniti a un bambino. L’autore non lo fa banalizzando il concetto! Il volume è pensato per bambini ma godibile da qualsiasi mente curiosa delle evoluzioni che il pensiero attraversa quando si confronta con i numeri.

A Plpl2018 invece mi era capitato di incontrare uno scrittore romano che è anche insegnante di matematica. O forse è più corretto dire un ingegnere che fa l’insegnante e cerca di raccontare con la sua vita la matematica. E ne scrive anche, cosi tanto per non farsi mancare nulla. Si chiama Marco Monti e ha scritto un libro intitolato “Numeri in Rivolta” (Haiku Edizioni). Se siete fortunati o fortunate potrebbe capitarvi di incontrarlo a Roma in qualche fiera domenicale, e potrete chiedergli di scrivervi qualcosa nella lingua dell’algebra. Oppure, se avete tempo, inseritevi nelle fila dei suoi capitani, per aiutarlo a costruire il più grande Triangolo di Sierpinsky del mondo!

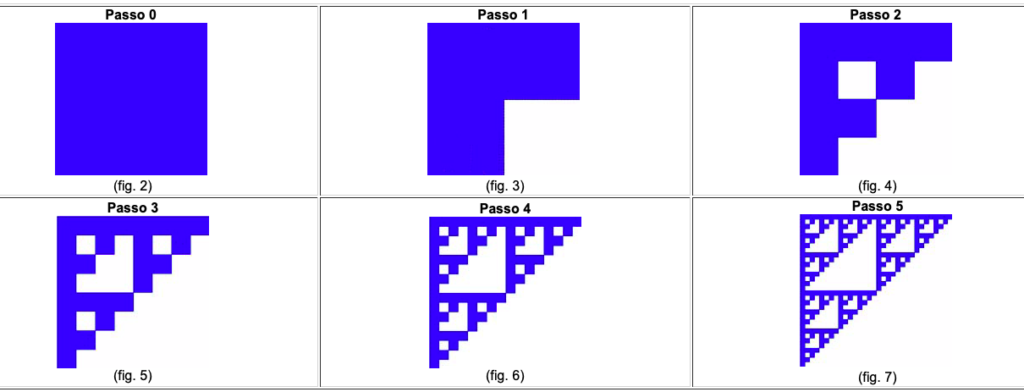
Questo triangolo, che prende il nome dal matematico Wacław Sierpiński, il primo a studiarne le proprietà nel 1915, è uno dei primi frattali studiati. La sua costruzione avviene con una serie di rimozioni: si inizia con un quadrato pieno da cui si rimuove un quadratino di lato pari alla metà del quadrato iniziale, in modo da ottenere una figura formata da tre quadrati. Da ciascuno di questi quadrati si elimina il quadratino in basso a destra e si ottiene una figura formata da nove quadratini. E così via fino al risultato finale. Un po’ come quando si cita Michelangelo e la sua frase sul blocco di marmo, per cui la creazione dell’opera d’arte è procedere per sottrazioni, togliendo il superfluo e facendo emergere quello che è già intrinseco nella materia informe.

Di numero in numero, ho ritrovato poco tempo fa uno dei libri che più mi ha aiutata, quando ero tra i banchi del liceo e non sapevo ancora cosa avrei fatto da grande. Non che lo sia diventata, grande. Ho perso il filo tante volte, nel tentativo di trovare il mio posto nel mondo. E questo mi riconduce alla questione degli irrazionali e della radice di due. Che è ben raccontata in due paginette di quel bel libro in testa alle classifiche della divulgazione sulla matematica, intitolato appunto “Che cos’è la matematica. Introduzione elementare ai suoi concetti e metodi”, di Richard Courant e Herbert Robbins (Bollati Boringhieri). A suo tempo lo avevo trovato imprescindibile, e lo è ancora oggi, per appassionarsi alla matematica partendo da qualsiasi livello. 

Nelle ultime settimane invece, e vado a chiudere con un pensiero che non può finire, mi sono imbattuta in un piccolo gioiello di letteratura matematica. Lo sto leggendo a dosi omeopatiche, perché l’autore mi intimidisce, come fanno i grandi della letteratura. Si tratta di David Foster Wallace e del suo “Tutto, e di più. Storia compatta dell’∞”, nella traduzione di Giuseppe Strazzeri e Fabio Paracchini (Codice Edizioni). Lo scrittore, romanziere, autore di “Infinite Jest (Einaudi) e studioso di matematica, da quella delle alte sfere a quella dei paradossi linguistici, inizia e non so ancora se termina, un racconto sulla storia di un’entità da paura, un mostro o una bruttura per i pitagorici, che lo escludevano dalle sfere della conoscenza con presupposti basati sul limite. 

In questo mio tempo di ritorno alla scuola, mi piacerebbe che i limiti fossero come un cambio di ora e di classe. E che l’incastro delle ore fosse dettato dall’amore. Come nello sguardo e nelle azioni della bella insegnante di matematica, nel film “La Scuola”. Colei che è responsabile degli orari di tutti, capace di creare l’incastro perfetto delle ore, certa di dimostrare amore a chi non se ne accorge, non lo merita forse? È distratto da altro, o è troppo preso da se stesso e dalle proprie insicurezze. Lei è Anna Galiena e lui è il povero insegnante di lettere, ovvero Silvio Orlando, che capisce quando ormai è troppo tardi, l’estate alle porte. A fine anno, scrutini ormai terminati, rimane solo nella scuola deserta, unica compagnia il ronzio della mosca Cardini, l’alunno irraggiungibile, perennemente assente, eppure presente. Ha perso l’occasione di riconoscere l’amore, ricambiarlo per quello che era, abbandonandosi all’irrazionale sentimento, che solo apparentemente non ha una collocazione, un punto sulla retta, ma in realtà è ovunque e comunque, basta riconoscerlo, riceverlo, ricambiarlo e lasciarcene inviluppare.